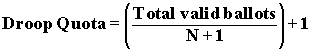
Supplemental notes on the Cambridge PR elections

What is the election quota and what is its purpose?
Many people will say that the election quota is the number of ballots a candidate must eventually receive in order to be elected. Though this usually is the case, it misunderstands both the purpose and the definition of the election quota. The real story is this:

Election Quota = the maximum number of ballots a winning candidate may retain

One thing is certainly clear – only winning candidates will ever have more than the election quota of ballots, so if a candidate receives that many ballots, he or she will be elected. It is not, however, necessary for a winning candidate to reach the election quota. This occasionally happens for candidates elected in the last round of the tabulation of ballots. More importantly, the election quota is used to ensure that voter constituencies receive their proportional share of representation. If one candidate was the overwhelming favorite within a particular constituency, that candidate would likely receive a disproportionately large share of #1 preferences. If that candidate were permitted to retain all of those ballots, it is quite possible that other candidates favored by that constituency might not be elected. The result would be that this constituency would then be underrepresented and effectively penalized due to the great popularity of one of its candidates. The election quota allows for the transfer of surplus ballots to help elect other candidates also favored by this constituency - an essential element of proportional representation.

How is the election quota determined?
Historically, the election quota was simply the total number of ballots cast divided by the number of candidates to be elected (rounded up, if necessary). This was known as the Hare Quota - originally devised by Thomas Hare (1806-1891), one of the earliest supporters of STV. Henry Richmond Droop (1832-1884) later argued that in small elections using the Hare Quota (typically a convention), the election could be "gamed" by political parties to gain a marginal advantage by caucusing in advance of the vote to ensure that their members did not "waste" any votes on their most popular candidates. He devised what is now commonly referred to as the Droop Quota. This is basically the minimum number of ballots necessary to elect a candidate that will not result in electing too many candidates (more than are supposed to be elected in the given election). The Droop Quota is used in virtually all modern implementations of Single Transferable Vote (STV) elections.

For example, if 9 candidates are to be elected and if the election quota is chosen to be any number in excess of 10% of all valid ballots, then the first 9 candidates to reach the election quota will together account for in excess of 90% of all ballots, and it will be impossible for any other candidate to be elected. If there are N candidates to be elected, then the Droop Quota is chosen as follows:

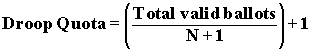
It should noted that in this formula we first calculate the largest whole number for the expression in parentheses and then add 1 to this value. In the case of a fraction this is the same as just rounding up, but in the case where the quotient is a whole number it is necessary to add 1 to guarantee that no more than N candidates are elected. For example, if there were 20000 valid ballots cast in an election to determine 9 city councillors, the Quota would be 2001. If there had been 19995 valid ballots cast, the Quota would be 2000.

The Cincinnati Method for surplus distribution
The technique used by Cambridge for selecting ballots to transfer from a candidate’s surplus to bring the candidate down to quota is called the "Cincinnati Method". The method is as follows: The ballots of a candidate (as determined by #1 choice) with a surplus of ballots (more than the election quota) are numbered sequentially in the order in which they have been counted (that is, in the sequence dictated by the random draw of precincts), and then every nth ballot is drawn and transferred to a continuing candidate (according to next available preference) until the original candidate is credited with ballots equal to the election quota. The integer n is the nearest whole number computed by the formula

A ballot selected by this method that does not show a preference for a continuing candidate is skipped and remains with the original candidate. If not enough ballots are removed when ballots n, 2n, 3n, .... have been transferred, the sequence starts again with n+1, 2n+1, 3n+1, ....

Comments:
It's important to stress that the #1 Choice of any voter is overwhelmingly the most important choice. For most voters, that's exactly where the ballot will end up without any need to consider any secondary or other preferences. The basic idea is that the only ballots that might ever need to be transferred are (a) those for which the #1 Choice has more than are needed to be elected; and (b) those for which the #1 Choice is defeated at some point in the vote tabulation. In the latter case, the intent is to ensure that the voter has additional opportunity to have his or her ballot counted toward another candidate who may still need that vote in order to gain election. In a typical election, few candidates will have a surplus of ballots and the surplus is usually relatively small, so the somewhat random aspect of surplus distribution generally has only a minimal effect on the election outcome. In a very close election, it could matter.

The Cincinnati Method is not the only method to transfer surplus ballots. There are, arguably, better ways available which do not depend upon which ballots are drawn or in which order they are counted. Cambridge is, however, in the position where we must abide by a 1938 law (Mass. General Laws, Chapter 54A) that restricts our methods for redistributing surplus ballots to systems that were in use somewhere in the United States at that time. Without a doubt, it is this issue of how surplus ballots are chosen for redistribution that is always the most difficult to explain and the hardest for people to accept.

Cambridge's choice of the "Cincinnati Method" is named after the place in the United States that was using this method in 1938. Other methods for surplus distribution are named according to the cities in which they were once used (in 1938), e.g. the "Boulder Method" that was once used in Colorado.

For example, let's say that there are 20,000 valid ballots cast in the election and Candidate A gets 2700 #1 votes. The election quota will be 10% of all valid ballots rounded up to the next integer (2001). This means that Candidate A will have a surplus of 699 ballots. Divide 2700 by 699 and you get about 3.86, so the "integer" is n = 4. This means that you pull every 4th ballot starting from the beginning, i.e. in sequence, the 4th, 8th, 12th, etc. If you pull a ballot that has no available other ranked choices, you pass it by and continue. At some point you may reach the end of the 2700 ballots and still need to pull more ballots in order to reduce to quota. In that case, you go back to the start and keep pulling the ballots immediately following the original sequence, i.e. the 5th, 9th, 13th, etc. At some point you'll get down to quota.

It's quite possible that another candidate may reach quota as surplus ballots are being transferred (or in later rounds as candidates are defeated and their ballots transferred to next available preference). If so, the instant that candidate reaches quota, he is no longer eligible to receive ballots and any further ballots will be transferred to the next candidate listed who is eligible to receive.

The Cincinnati Method (which I believe Cambridge adopted in 1973) is not my preferred choice. The method that is generally adopted these days is known as "fractional transfer" and is best characterized as transferring a fraction of ALL of a winning candidate's ballots to the next available ranked choices on those ballots. In the example above, the winning candidate would retain 2001/2700 of every one of his ballots giving him a total "weight" of 2001. Meanwhile 699/2700 of every one of his ballots would be transferred to candidates ranked next on each of those ballots. During the subsequent Rounds of the election process, each ballot is counted with its associated weight. The other difference is that when any candidate reaches quota during a Round, he will still be eligible to receive ballots through the end of the Round. This is necessary so that ballot order does not matter. At the end of the Round, any surplus would then be redistributed in the manner described above.

This method, although it does not involve "whole ballots", has the great advantage of being completely independent of the order of the ballots. In a system using fractional transfers, all of the ballots could be shuffled at the beginning of the Count and it would have no effect on the outcome. This method is actually the default option of the tabulation software we use in the Cambridge elections. We have to override that default option by instructing the software to use the "Cambridge Rules" instead. -- Robert Winters

Voting with the choice voting form of proportional representation - a system that makes sense for non-partisan elections - is simple.

1. You decide which candidates you would like to see elected.
2. You rank those candidates in order of preference - knowing that a lower-ranked choice will never hurt the chances of a higher-ranked choice.

Your vote will be counted toward the highest candidate on your ranked list who can be helped by your vote. As many people as mathematically possible will elect one person - most voters will help elect one of their top two choices.

Coalitions of candidates can run as a team (or what we call a "slate" here in Cambridge) and try to win a proportional share of seats. In general, this is an important consideration. It's not just about individual candidates reaching out to get their quota of votes. For example, if there was one issue of great importance to all voters and if a majority of voters favored one position on that all-important issue, there may be some incentive for candidates on either side of that issue to run as a coalition in order to try to win a majority of seats.

Cambridge's proportional representation elections require that the names of the candidates be rotated in alphabetical order on the ballot so that each candidate appears in the desirable top-of-the-ballot position on an approximately equal number ballots.

Instructions to Voters
Mark your choices by completely filling in the numbered ovals using a black pen (provided).

Fill in the number 1 oval next to your first choice.

Fill in the number 2 oval next to your second choice.

Fill in the number 3 oval next to your third choice, and so on.

You may fill in as many choices as you please.

Fill in no more than one oval per candidate.

Fill in no more than one oval per column (ranking).

To vote for a write-in candidate:
Fill in a numbered oval next to the name you have written (or the sticker you have affixed to the ballot), showing your choice as a number for a candidate.

Record write-ins from the top line down.

If you spoil your ballot, return it for cancellation to the election officer in charge of the ballots and get another from such officer. (Under Massachusetts law, a voter is permitted up to two spoiled ballots after which the third ballot must be cast.)

Cambridge's optical scan voting machines will reject any ballot with an overvote (for example, #1 votes given to two different candidates). The scanners are also programmed to set aside any ballots with write-in candidates or any apparently blank ballots for inspection by the election commissioners the following day. These "auxiliary ballots" will then the tabulated when voter intent has been determined. Only after all ballots have been recorded will the final ballot tabulation take place (usually the afternoon or evening of the day after Election Day).

How the PR quota system works (simplified)
Under PR a candidate needs to win a certain proportion of the the votes to be elected. This winning fraction of the votes is referred to as the “quota”.

The quota is determined by dividing the total number of valid ballots cast by one more than the number of positions to be elected, then rounding up or adding one to the resulting dividend.

Thus, to elect 9 City Councillors, the total number of valid ballots cast is divided by 10.

For example, if 25,000 valid ballots are cast for City Councillors, the quota will be 2,501 (25,000 divided by ten, plus 1).

How the ballots are counted
The count begins with the sorting of ballots by the first preference shown. This is known as the “First Count.”

Any candidates who reach the necessary quota with Number 1 votes are declared elected. Any extra ballots they receive beyond the quota, referred to as the “surplus,” are redistributed to the candidates marked next in preference on those surplus ballots according to the “Cincinatti Method.”

After the surplus is redistributed, the count continues with the elimination of those candidates who received fewer than fifty votes in the first count. Their ballots are redistributed to the remaining unelected candidates according to the next preference marked.

[The simultaneous elimination of candidates with less than 50 votes is a Cambridge-specific rule. The New York City School Boards used a different rule and there would be virtually no difference if this rule were eliminated altogether. In the early days of Cambridge's use of this system, the intent was to eliminate all of the very fringe candidates at once, but there is a lot of flexibility in how you may choose to do this.]

After each distribution, the candidate having the lowest number of votes is eliminated and his/her ballots are redistributed to the next indicated preference among the remaining unelected candidates. In the event of a tie, the relative position of the candidates in the previous Round determines which candidate will be next eliminated.

As candidates “reach quota” through the addition of redistributed ballots to their totals, they are declared elected and no further ballots are transferred to them.

This process continues until all candidates have been eliminated except the nine winners.

The School Committee election is governed by the same rules except that the election quota is one-seventh of all valid ballots and there will be six candidates elected.

Robert Winters
Cambridge, MA
Robert@rwinters.com
617-661-9230
Cambridge Civic Journal: http://rwinters.com